逻辑门(Logic Gates)是在集成电路(Integrated Circuit)上的基本组件。简单的逻辑门可由晶体管组成。这些晶体管的组合可以使代表两种信号的高低电平在通过它们之后产生高电平或者低电平的信号。高、低电平可以分别代表逻辑上的“真”与“假”或二进制当中的1和0,从而实现逻辑运算。
此外,逻辑门也可以使用继电器实现,早期的计算机就是使用它来完成的。
先介绍基本的逻辑门,并附上它们的真值表,虽然很简单,但是计算机复杂的功能都是由这些简单的逻辑门组成的。
与门
| A | B | out |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
即只有同时输入都为真是,输出才为真,门里面的真假值是使用高低电平来表示的,例如0V为低电平表示假,5V为高电平表示为真, A,B表示输入,out表示输出。

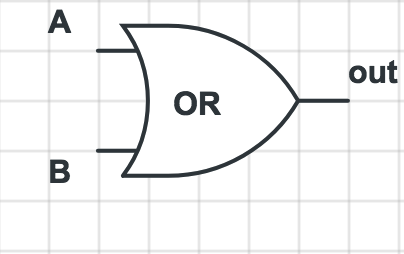
| A | B | out |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
即有一个为真,输出就为真。
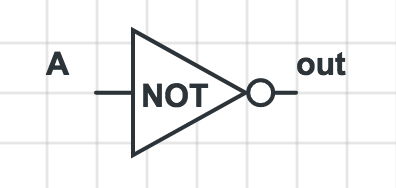
| A | out |
|---|---|
| 0 | 1 |
| 1 | 0 |
即输入与输出相反
其实到这里,逻辑基本的门就已经介绍完了,剩下的门只不过这三种门的组合。
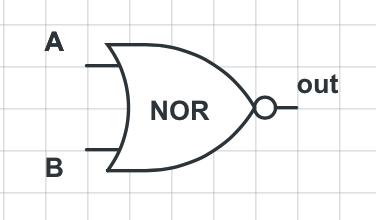
| A | B | out |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
由或门,非门组成,只有两个输入都为假时,输入才为真。
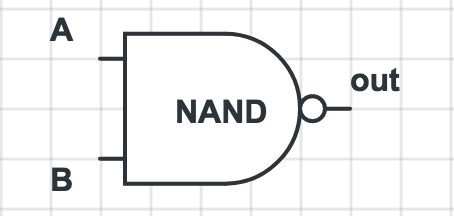
| A | B | out |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
由与门,非门组成,只有两个输入都为真时,输出才为假。
| A | B | out |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
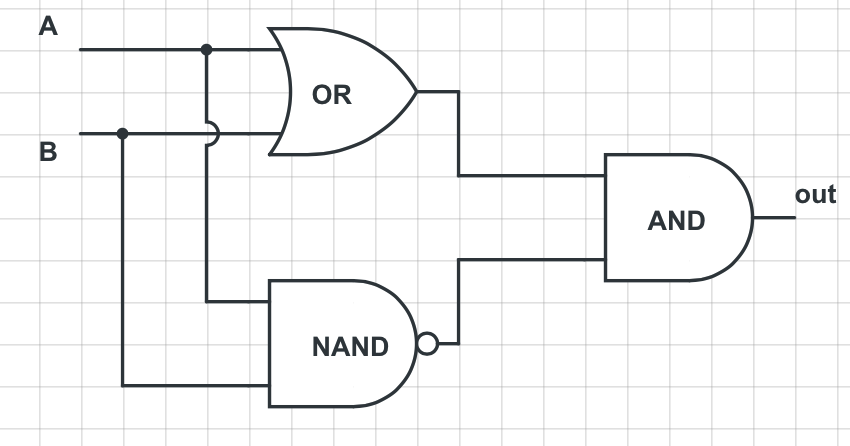
异或门由或门,与非门,与门组成,有特定的电气符号:

利用上面介绍的基础逻辑门,就可以实现二进制加法器,先来看一下一位的二进制加法器怎么实现。
一位二进制加法很简单,可以将结果分为进位位与加和输出为:
| a | b | 加和位 | 进位 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
观察加和位的输出与进位的输出,加和位可以使用异或门来实现,进位可以使用与门来实现,将这两个门连接在一起就是这个样子:
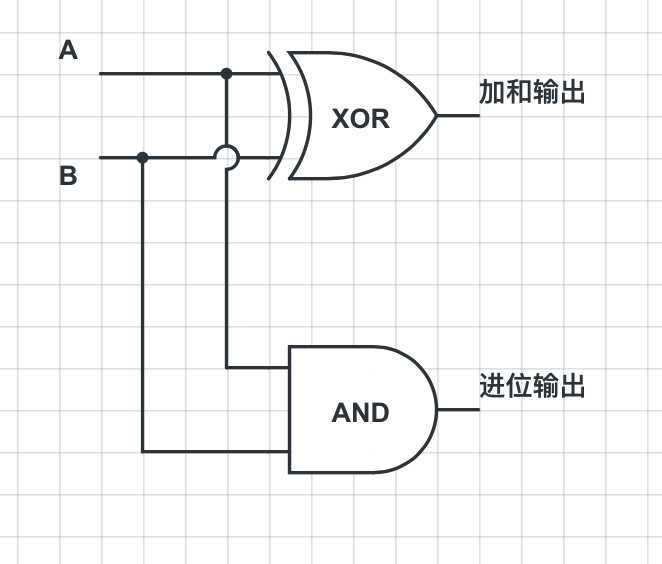
刚好和上面的真值表的输出一致。
这个被称为半加器,因为大多数二进制加法都是多于一位的,要考虑其低位的进位。
为了简单,简化的半加器的符号:
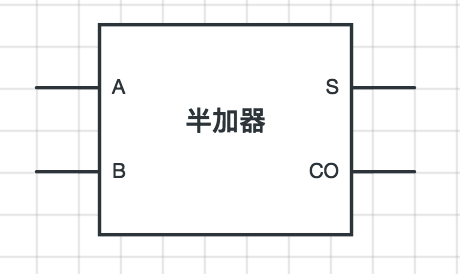
利用两个半加器就可以组成一个全加器:
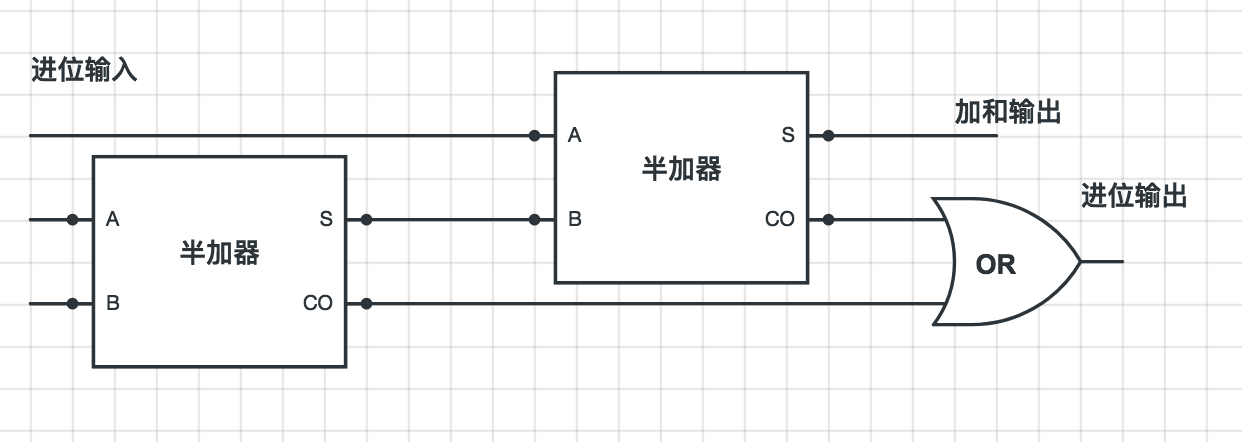
为了简单,简化的全加器的符号:
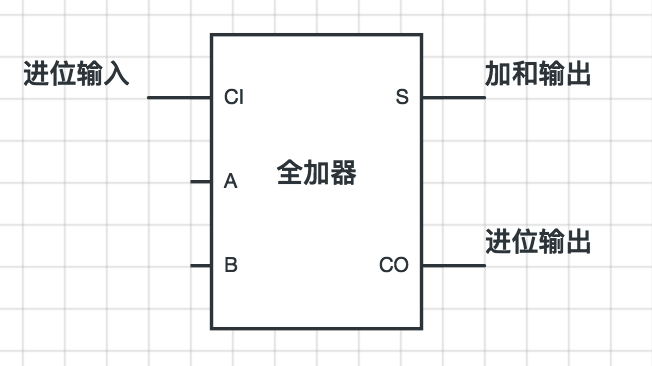
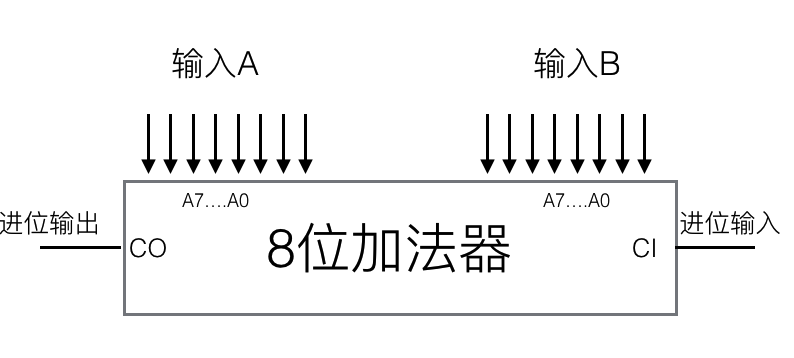
得到了这全加器,很容易就可以扩展二进制加法器的位数8位,16位,32位….例如扩展为8位,8个全加器“串联”在一起即可,每一位的进位输出是下一位的进位输入。下图表示8位的加法器图示:
由于二进制的减法涉及借位复杂的操作,实现起来电路较为复杂,通常是利用加法来实现,没错了,就是利用将减数求补码与被减数相加来实现,可以将符号位与数值域统一处理。下面介绍实现的原理。
求253-176的运算结果:
1111 1101 - 1011 0000
= 1111 1101 - 1011 0000 + 1 0000 0000 - 1 0000 0000
= 1111 1101 - 1011 0000 + 1111 1111 + 1 - 1 0000 0000
= 1111 1101 + (1111 1111 - 1011 0000 + 1) - 1 0000 0000
//被括弧的这个式子就是176的补码
= 1111 1101 + 0100 1111 + 1 - 1 0000 0000
//其实加法器只做到了这一步,进位后最高为溢出,剩下的就是我们想要的结果
= 1 0100 1101 - 1 0000 0000
= 0100 1101
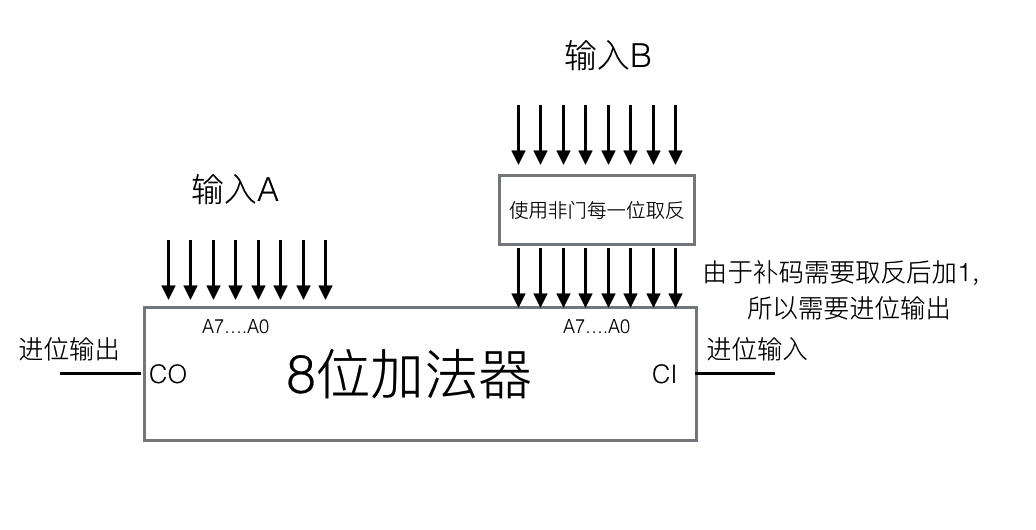
所以我们只需要在原来加法器的基础上,将减数进行补码运算即可。
上面我们已经完成了二进制的加法与减法,现在我们需要将我们的运算结果存储起来。
我们将非门的输入与输出连接起来,得到这样的一个电路:
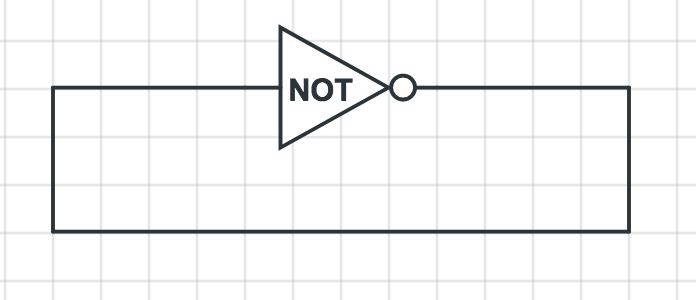
由于非门是利用继电器的机制实现的,所以这个电路出现01交替的输出,频率取决于非门通断的速度。
可以得到这样一个过程:
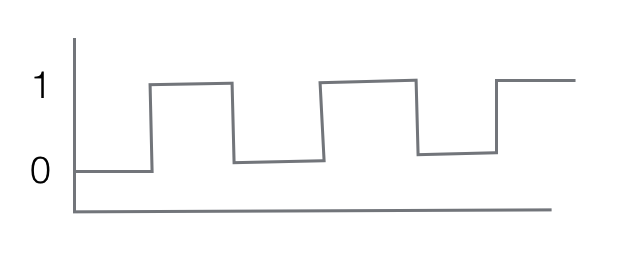
可以使用触发器来保存位的信息,能够保存一位的信息,就可以扩展到保存多位的信息。
RS触发器的电路如下,由两个或非门组成:
真值表:
| S | R | Q | Q` |
|---|---|---|---|
| 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 0 | Q | Q` |
| 1 | 1 | NA | NA |
输入端S可以用来置位,输入端R可以用来复位。当我们向输入端输入信息之后,RS触发器就可以记住其状态。
待续。。。